type
status
date
slug
summary
tags
category
icon
password
煤气管网平衡模型
背景：
通常能源管控系统的调度功能是依托专家规则进行调度功能开发，调度指令依据能源产耗平衡差异现状，结合现场调节设备的调节能力生成具体调度指 令，下发给到工艺操作班组， 并收集现场调度指令执行情况进行持续跟踪。仅 靠基于规则的调度功能在能源产耗动态平衡的精细化调节程度和能效量化优化 程度上不足，因此对建立能源管网模型， 基于管网模型约束实现实时能源平衡 管理和动态调度提出切实需求。
本项目中将以模块化方式构建管网模型， 实现结合产气预测，耗气预测等 的 AI 智慧调度功能 ，具体模型方案如下：
以煤气管网为例， 通过煤气管网的拓扑连接关系， 围绕着管网的源网荷储 等重点设备，分析管网模型的最小建模单元，包含管道， 泵， 阀门，产气设备， 用气设备，储气设备，并选定对应的建模方式。
1 、产气设备：产气设备（如高炉 、转炉）在管网平衡模型中煤气发生属于 不受控模型，应利用现场数据，通过数据驱动模型，计算得到煤气的生成流量 等关键信息，并将其作为管网模型确定性输入条件；
2 、输运设备：该类模型包含管道，阀门，泵等重点设备模型。该类设备属 于被动响应模型。管道模型采用机理建模的方式完成，在保留模型的参数可配置的方式，进一步利用现场数据，完成参数的拟合。管道将利用流体力学建模 理论，以伯努利方程为基础，构建通用管道的模型，通过设定沿程阻力系数， 模拟压力和流量之间的关系。 阀门和泵模型则以性能模型方式完成开发， 阀门 基于阀门和泵的设计信息，获取流量特性曲线信息， 并与管道模型耦合求解， 完成压力-流量的关系计算；
3 、用气设备则分为流量受控用气设备，重点包含工艺侧用气设备， 如热风 炉 、加热炉。该类设备模型，应利用现场数据，通过数据驱动模型， 计算得到 煤气的生成流量等关键信息，作为管网模型的确定性输入。针对不受控用气流 量设备，应联合阀门管道等设备，通过压力计算流量的方式，计算该类型设备 的流量信息，如放散燃烧火炬，以及锅炉等；
4 、储气设备：储气设备的属于典型的压力决定流量设备，应联合管道阀门 以及储气柜压力信息，计算得到各煤气柜流量进出信息；
5 、管网平衡模型，由于要充分考虑平衡模型方程求解的时效性等问题，结 合管网压力属于快速反应的特点，拟选用稳态建模的方式构建管网平衡模型 。 管网模型因考虑管网质量守恒 、能量守恒等约束条件 ，通过求解管道平衡模型 的方程，计算连接到管网中各节点的压力流量等信息；
6、针对高炉转炉以及工艺侧用气设备模型，将沿用河钢数字方已经开发的 数据驱动的模型，直接获取流量信息，避免重复开发。
目标：
- 确认管网平衡模型数学描述，能源管网系统指标
- 管网模型输入输出数据，模型接口
- 开发管道，阀门，泵，煤气柜模型
- 场景下的管网拓扑模型
- 离线测试
前置理论基础：
- 流体力学基础：伯努利方程、沿程阻力计算、局部阻力计算
- 网络拓扑理论：节点-支路表示法、回路分析方法
- 数值求解方法：牛顿-拉夫森法、哈代-克罗斯法等网络平衡求解算法
关键材料与数据：
- 煤气管网拓扑图和设计参数
- PFD图和真实历史数据
- 各节点的测点位置和数据采集方式
初步计划：
第1周:
- 熟悉项目背景与需求
- 收集并整理管网设计数据
- 学习流体网络建模理论
第2-3周:
- 定义模型接口规范
- 撰写数学描述文档
- 构建基础组件模型(管道、阀门、泵)
第4-6周:
- 实现管网平衡核心算法
- 整合各子模型
- 初步单元测试
第7-8周:
- 系统集成测试
- 与实际数据对比验证
- 模型参数优化调整
第9-10周:
- 完成模型文档编写
- Python代码打包为pyc文件
- 准备最终交付物
流体力学三大基本方程：
- 连续性方程（质量守恒定律），单位时间内控制体内质量的增量等于流入与流出质量的代数和
- 动量方程（牛顿第二定律），流体微单元的动量变化率等于作用力（压力、张力、重力、其他外力）的总和
- 能量方程（热力学第一定律），流体内能、动能、压力功与热交换的守恒关系
流体力学理论基础
雷诺数
判断流动是层流还是湍流
其中
- 为流体密度（）
- 为流体运动速度（）
- 为流场中的某种特征尺寸（如管道直径，）
- 为流体的运动粘性系数（ 或 ）
雷诺运输定理
力学中描述运动的方法
- 拉格朗日法：物体与环境之间发生力的作用从而改变自身的运动状态（适用于固体力学分析）
- 欧拉法：流体经过一个固定空间时发生的变化以及与这个空间的相互作用（适用于流体力学分析）
雷诺运输定理表示某一时刻控制体（CV，即固定空间）的变化和体系(SYS，即质点团)的变化之间的关系，因此可以实现用于将”一个随物质移动的系统”的分析，转化为“一个固定空间区域”上的分析
其中
- 为某种守恒量（如质量、动量、能量等）
更一般的形式
其中
- 为单位体积的某个物理量（如动能、温度等）
- 为控制体内的微元体积
- 为控制面（流出横截面）面积
- 为流体速度矢量
- 为控制面外法向量
物质导数(雷诺运输定理的微分形式，表示欧拉坐标系下一个质点物性随时间的变化)
其中，右侧第一项称为当地项，第二项称为对流项， 称为 nabla 算子，是向量微积分中用来计算标量场梯度、向量场散度和旋度的统一微分运算符，其展开形式为
粘性力
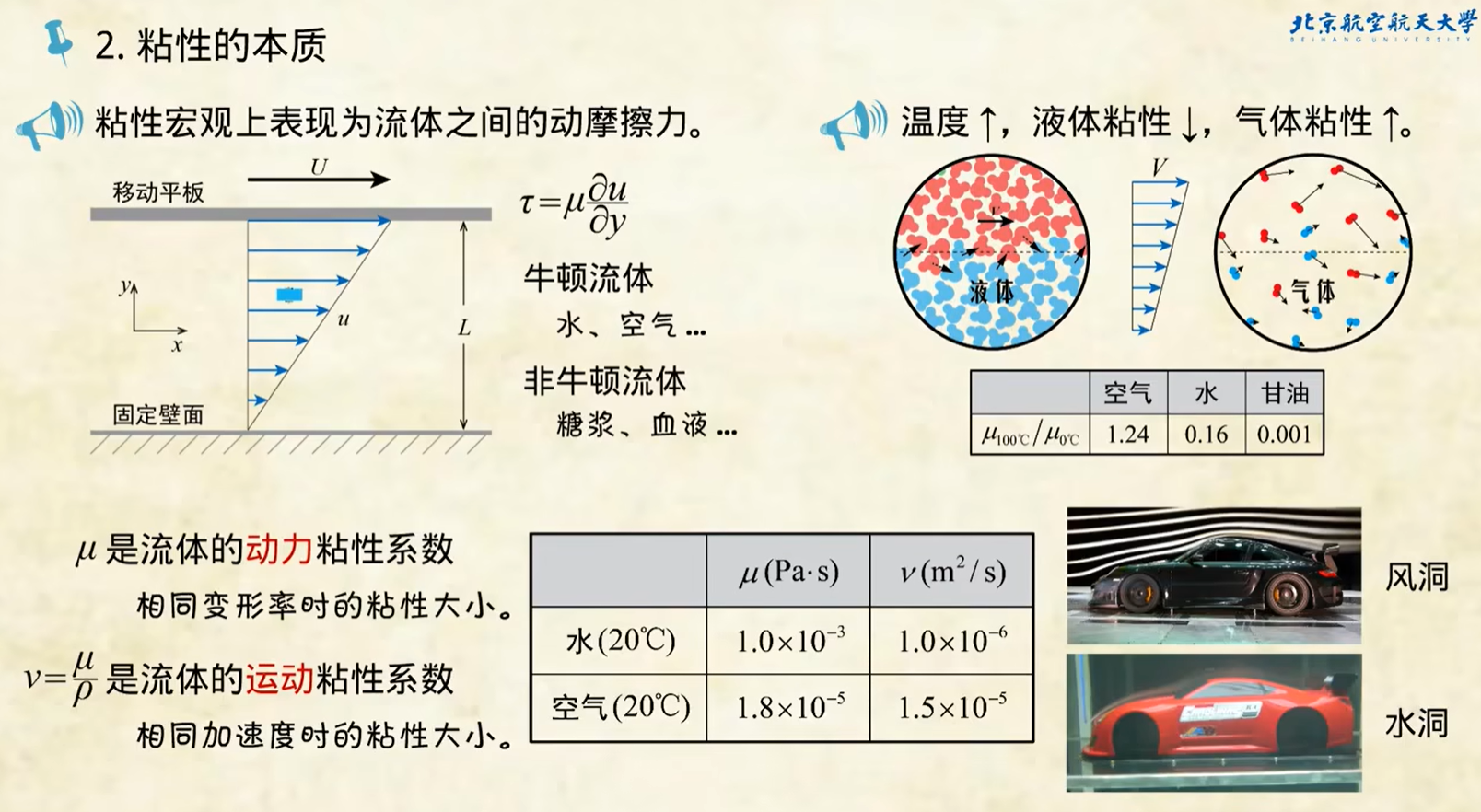
工程上常用以下几类压降（沿程阻力）公式
公式名称 | 适用流态 | 是否考虑可压缩性 | 特点和应用场景 |
达西–魏斯巴赫 (Darcy–Weisbach) | 可压/不可压流皆可 | √（可扩展） | 最通用的阻力压降公式，适合任意管道类型，可数值迭代可压缩性 |
Weymouth 公式 | 湍流、长管段 | √ | 简洁、稳定，适用于高压（>1MPa）天然气管道干线 |
Panhandle A/B | 湍流、高雷诺数 | √ | 类似 Weymouth，适用于中高压气体管线 |
AGA/API/IS 公式 | 湍流 | √ | 各国标准化公式，用于商业气体工程（常用于天然气） |
达西-魏斯巴赫公式
其中，摩擦系数 f 的值根据moody图选择，默认取0.02
对于理想气体，考虑气体状态方程
推导质量流量计算公式：
压缩性
连续方程
动量方程
纳维-斯托克斯方程
问题收集
管道中的煤气是否应该考虑压缩性影响？
实际场景，煤气管网跨度大，沿程压降累积显著，煤气柜影响压力波动，温度压力影响密度变化，因此仍需考虑压缩性
煤气管网流体分析应该采用积分法还是微分法？
欧拉法中的积分方法又被称为控制体积（CV）分析方法
积分法
- 通常需要较少的计算资源，适合工程中的实时或快速预测
- 只分析控制体表面的受力和进出控制体的流体的性质，而不需要研究控制体内部的变化
微分法
- 复杂度高，通常计算量大，适合离线或高精度需求的情况
- 逐点求解流场的压力、速度分布，再积分得到宏观参数
积分法（控制体分析法）的优势在于处理整体问题，计算效率高，适合宏观预测，且能通过选择控制体简化问题，因此优先选择积分法
管网分析算法
水头损失
水头损失本质是单位质量流体因摩擦或局部阻力而损失的能量，工程中采用等效水柱高度（米）作为单位
达西-韦斯巴赫（Darcy-Weisbach）公式主要用于计算不可压缩流体（或轻微可压缩气体）在完全发展的湍流或层流状态下，流经直圆管时的沿程摩擦压头损失
其中
- 为水头损失（m）
- 为摩擦阻力系数（无量纲）
- 为管长（m）
- 为管径（m）
- 为平均流速(m/s)
- 为重力加速度（9.81m/s）
根据体积流量与流速的关系
带入达西公式后简化
其中
- 为沿程阻抗
- 为体积流量（m/s）
对于局部损失，由弯头和配件处增加的湍流引起，通常用一下经验公式
其中
- 为局部损失系数
具体数值参考下表
配件 | 局部损失系数 |
Globe valve, fully open球阀，全开 | 10.0 |
Angle valve, fully open角度阀，全开 | 5.0 |
Swing check valve, fully open摆动式止回阀，全开 | 2.5 |
Gate valve, fully open闸阀，全开 | 0.2 |
Short-radius elbow 短半径弯头 | 0.9 |
Medium-radius elbow 中半径弯头 | 0.8 |
Long-radius elbow 长半径弯头 | 0.6 |
45 degree elbow 45 度弯头 | 0.4 |
Closed return bend 闭合回弯管段 | 2.2 |
Standard tee - flow through run标准三通 - 流量通过直管段 | 0.6 |
Standard tee - flow through branch标准三通 - 流量通过支管 | 1.8 |
Square entrance 方形入口 | 0.5 |
Exit 出口 | 1.0 |
简化后
因此总水头损失为
在管网中，设 为连接节点 和 的管道中的体积流量，当水流从 流向 时为正，反向流动为负，管道的摩擦水头损失与流量之间的关系可表示为
其中
- 为水头损失（带方向）
- 为沿程阻力系数
- 为流量指数，使用达西公式时n=2
- 为局部损失系数
如果管网中流体为气体，一般更关心的是压力损失即压降，其在气体数据变化表达上更为直观
压力损失
对于不可压缩流动（液体），压力损失可直接由水头损失换算
对于可压缩流动（气体），其密度随压力和温度变化，常用
其中
- 为气体当量常数（J/kg·K）
- 为压缩因子
- 为气体温度（K）
- 为体积流量， 为质量流量
节点-管道关联矩阵
节点矩阵本质是一个稀疏矩阵，用于表示每条管道与两个节点的连接关系
假设有 个节点， 条管道，构造一个 的关联矩阵
对于第 个节点和第 条管道：
能量守恒
在管道中，流动方向上的压差 = 流动阻力引起的压损
节点矩阵的表示形式为：
质量守恒
在管道中，对于每个节点 ，所有相邻节点j的管段流量之和 = 节点i需求量，流入节点 流量值为正，流出节点 流量值为负
其中
- 为节点 处已知的需求流量，必须在该节点处提供
节点矩阵的表示形式为：
动量守恒
在管道中，将气体视为稳态一维流动，动量方程为
其中
- 第一项为压力梯度，沿x方向的压力变化
- 第二项为惯性力项，反应加速度效应，稳态流动中视为0
- 第三项为重力分量， 为管道倾斜角度
- 第四项为摩擦阻力项，由达西公式得到
雅可比矩阵
雅可比矩阵是一个多变量函数的偏导数组成的矩阵，描述局部变化率，常用于非线性系统的牛顿法求解
给定一个多元向量函数：
它的导数对应的雅可比矩阵表示如下：
牛顿法
函数 的根是其与 轴的交点，迭代求解根的步骤如下
- 给定一个初始值
- 画出 在 处的切线
- 切线与 轴的交点
- 画出 在 处的切线
- …迭代逼近精确解
点 的切线斜率方程是
令
因此单变量中，牛顿法迭代公式表示为
在多元中，用泰勒展开的一阶近似
泰勒展开公式
核心思想：用多项式函数逼近任意光滑函数
设 在 处 阶可导，则
实际使用中，通常选前 项作为近似，如牛顿法取前两项（切线）近似
误差由余项 表示
- 拉格朗日余项：
- 佩亚诺余项：
令
残差
残差（Residual）表示近似解 与真实解 的误差
对于函数 ，残差是 ，即
对于方程组 ，残差是一个向量
其中
- 是第 次迭代的近似解
- 是第 次迭代的残差向量
采用牛顿法时，收敛判据常用残差范数小于某个容差 （工程上常用 ）
举例一：在管网中，直接采用经典牛顿法，根据能量守恒和质量守恒，构建出非线性方程组
构造雅可比矩阵
举例二：求解二维非线性方程组
- 定义
- 雅可比矩阵
- 每次迭代做
- 更新
⚠️ 注意事项
- 初值必须“足够接近”真正解，否则可能发散
- 雅可比矩阵可能稀疏、奇异，需要数值稳定的解法（LU 分解、SVD、迭代法）
- 可使用数值微分或自动微分近似雅可比
全局梯度算法（Thdini’s Global Gradient Algorithm）
一个高效、稳定地求解水力管网（水、气等管流）中的水头/压力分布问题的通用数值算法
步骤
- 构建雅可比矩阵，对每个节点计算
- 求解节点水头或压力稀疏线性方程组
- 更新节点水头或压力
- 对每条管道应用标量更新公式计算新的流量
相比于牛顿法直接求解水头和流量，GGA只以节点水头为主变量，流量单独更新，收敛快
雅可比矩阵的构建
为了构建非线性方程组，首先采用质量守恒方程
推导雅可比项
根据动量守恒方程
所以
为了明确 的符号，使用节点矩阵元素描述管段流量
简化后
- Author:风之旅人
- URL:https://www.hrmi.fun//article/gas-network
- Copyright:All articles in this blog, except for special statements, adopt BY-NC-SA agreement. Please indicate the source!
